Verhältnisse und Proportionen
Verhältnisse vergleichen Mengen, und Proportionen zeigen, dass zwei Verhältnisse gleich sind. Denk an Rezepte oder Karten!
Kurze Einführung
Verhältnisse helfen uns, Mengen miteinander zu vergleichen, wie z.B. das Verhältnis von Äpfeln zu Orangen in einem Obstkorb. Proportionen zeigen uns, dass zwei verschiedene Verhältnisse gleichwertig sind, wie beim Hochskalieren eines Rezepts für mehr Personen. Sie sind super nützlich, um Probleme im Alltag zu lösen, von Kochen bis hin zu Landkarten lesen! 🗺️
Haupterklärung
Was ist ein Verhältnis?
Ein Verhältnis vergleicht zwei Mengen. Stell dir vor, du hast 3 blaue und 2 rote Bälle. Das Verhältnis von blauen zu roten Bällen ist 3:2 (gesprochen 'drei zu zwei'). Das bedeutet, für je drei blaue Bälle hast du zwei rote Bälle. Wir können das auch als Bruch schreiben: 3/2. ⚽🏀
Was ist eine Proportion?
Eine Proportion sagt uns, dass zwei Verhältnisse gleich sind. Wenn du beispielsweise ein Kuchenrezept hast, das 1 Tasse Mehl und 1/2 Tasse Zucker benötigt (Verhältnis 1:1/2 oder 2:1), und du möchtest den Kuchen doppelt so groß backen, musst du auch die Mengen verdoppeln. Dann brauchst du 2 Tassen Mehl und 1 Tasse Zucker (Verhältnis 2:1). Die Verhältnisse 1:1/2 und 2:1 sind proportional zueinander. 🍰
Wie löst man Proportionen?
Oftmals musst du einen unbekannten Wert in einer Proportion finden. Zum Beispiel: Wenn 5 Äpfel 2 € kosten, wie viel kosten dann 10 Äpfel? Wir können das so aufschreiben: 5 Äpfel / 2 € = 10 Äpfel / x €. Um x herauszufinden, kreuzmultiplizieren wir: 5 * x = 10 * 2. Das ergibt 5x = 20. Teilen wir beide Seiten durch 5, erhalten wir x = 4. Also kosten 10 Äpfel 4 €. 🍎
Anwendung im Alltag
Verhältnisse und Proportionen sind überall! Beim Mischen von Farben (2 Teile Blau zu 1 Teil Gelb ergibt Grün), beim Vergrößern oder Verkleinern von Bildern (die Proportionen des Bildes müssen erhalten bleiben, damit es nicht verzerrt aussieht) oder beim Berechnen von Rabatten (20% Rabatt bedeutet, dass du 80% des Originalpreises zahlst). 🎨
Beispiele
- Kuchen backen: Ein Rezept sagt, du brauchst 2 Eier für eine kleine Kuchenform. Wenn du eine doppelt so große Form hast, musst du auch doppelt so viele Eier nehmen, also 4. Das Verhältnis von Eiern zur Kuchenform muss gleich bleiben!
- Landkarten lesen: Eine Landkarte hat einen Maßstab von 1:100000. Das bedeutet, 1 cm auf der Karte entspricht 100000 cm (oder 1 km) in der Realität. Wenn zwei Städte auf der Karte 5 cm voneinander entfernt sind, sind sie in Wirklichkeit 5 km voneinander entfernt.
- Saft mischen: Du möchtest Orangensaft mit Wasser mischen. Das Verhältnis soll 1:3 sein (1 Teil Saft, 3 Teile Wasser). Wenn du 200 ml Saft hast, brauchst du 600 ml Wasser, um das richtige Verhältnis zu erhalten. 🍹
Jedes Fach in 3 einfachen Schritten beherrschen
- Lernziel auswählen: Wählen Sie aus hunderten von Konzepten aus MINT, Wirtschaft, Geisteswissenschaften und beruflichen Kompetenzen. Zerlegen Sie komplexe Themen in überschaubare Einheiten.
- Durch Lehren lernen: Nutzen Sie unsere KI-gestützte Plattform, um Konzepte zu erklären, als würden Sie andere unterrichten. Entdecken und schließen Sie Wissenslücken sofort.
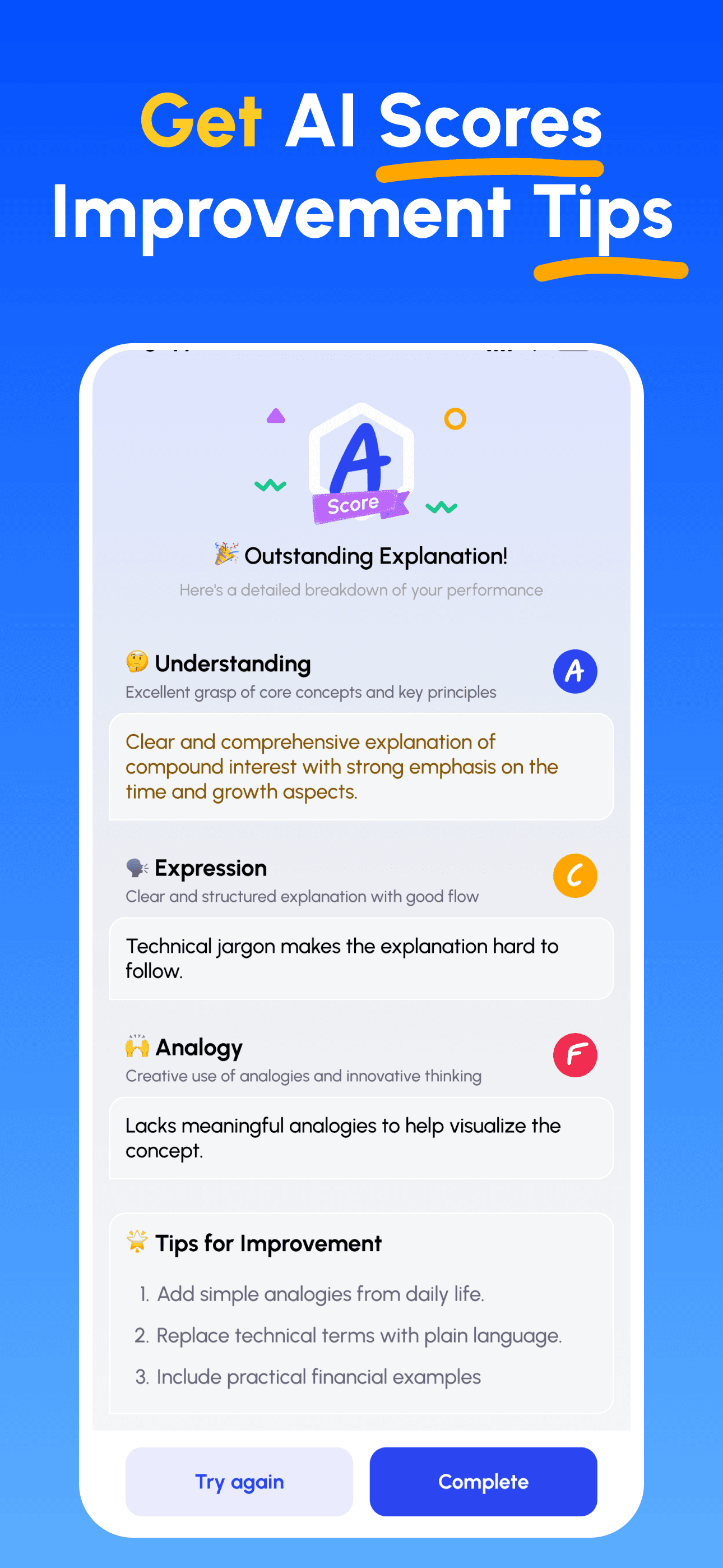
- Professionelle KI-Anleitung erhalten: Erhalten Sie sofortiges, detailliertes Feedback zu Ihrem Verständnis, Ihrer Erklärungsklarheit und Ihren praktischen Anwendungsfähigkeiten.
- Bewertungen prüfen & verbessern: Gezielte Tipps befolgen, Erklärung verfeinern und iterieren, bis Sie es einfach lehren können.
Feynman AI jetzt herunterladen
Starten Sie heute Ihre Reise zu besserer Kommunikation!