Wahrscheinlichkeitstheorie
Die Wahrscheinlichkeitstheorie sagt uns, wie wahrscheinlich es ist, dass bestimmte Dinge passieren.
Kurze Einführung
Die Wahrscheinlichkeitstheorie hilft uns zu verstehen, wie wahrscheinlich verschiedene Ergebnisse bei Ereignissen mit Unsicherheit sind. Es ist wie ein Werkzeug, um Vorhersagen zu treffen, auch wenn wir nicht alles genau wissen. Stell dir vor, du wirfst eine Münze – die Wahrscheinlichkeitstheorie hilft uns zu verstehen, warum Kopf oder Zahl ungefähr gleich wahrscheinlich sind.
Haupterklärung
Wahrscheinlichkeit als Zahl
Wahrscheinlichkeit wird oft als eine Zahl zwischen 0 und 1 ausgedrückt. 0 bedeutet, dass etwas unmöglich ist, und 1 bedeutet, dass es sicher passieren wird. Zum Beispiel hat eine faire Münze eine Wahrscheinlichkeit von 0,5 (oder 50%) für Kopf und 0,5 für Zahl.
Unabhängige Ereignisse
Manche Ereignisse haben keinen Einfluss aufeinander. Das sind unabhängige Ereignisse. Wenn du eine Münze wirfst, hat das Ergebnis des ersten Wurfs keinen Einfluss auf den zweiten Wurf. Die Wahrscheinlichkeit für Kopf bleibt immer 0,5.
Abhängige Ereignisse
Andere Ereignisse beeinflussen sich gegenseitig. Das sind abhängige Ereignisse. Zum Beispiel: Wenn du Karten aus einem Deck ziehst, ändert sich die Wahrscheinlichkeit, eine bestimmte Karte zu ziehen, nachdem du schon eine Karte gezogen hast. Wenn du eine Karte gezogen hast, sind weniger Karten im Deck, und die Wahrscheinlichkeit für die verbleibenden Karten ändert sich.
Berechnung von Wahrscheinlichkeiten
Um die Wahrscheinlichkeit mehrerer Ereignisse zu berechnen, multipliziert man oft die Einzelwahrscheinlichkeiten. Zum Beispiel, um die Wahrscheinlichkeit zu berechnen, zweimal hintereinander Kopf zu werfen, multipliziert man 0,5 (erste Kopf) mit 0,5 (zweite Kopf), was 0,25 (oder 25%) ergibt.
Beispiele
- 🎲 Denk an ein Würfelspiel. Die Wahrscheinlichkeit, eine 6 zu würfeln, ist 1/6, weil es sechs Seiten gibt und nur eine davon eine 6 ist.
- ☔ Wenn der Wetterbericht sagt, dass die Regenwahrscheinlichkeit 70% beträgt, bedeutet das, dass es in der Vergangenheit, bei ähnlichen Wetterbedingungen, in 7 von 10 Fällen geregnet hat.
- 🎫 Stell dir eine Lotterie vor. Die Wahrscheinlichkeit, den Jackpot zu gewinnen, ist sehr gering, weil es unglaublich viele mögliche Zahlenkombinationen gibt.
Jedes Fach in 3 einfachen Schritten beherrschen
- Lernziel auswählen: Wählen Sie aus hunderten von Konzepten aus MINT, Wirtschaft, Geisteswissenschaften und beruflichen Kompetenzen. Zerlegen Sie komplexe Themen in überschaubare Einheiten.
- Durch Lehren lernen: Nutzen Sie unsere KI-gestützte Plattform, um Konzepte zu erklären, als würden Sie andere unterrichten. Entdecken und schließen Sie Wissenslücken sofort.
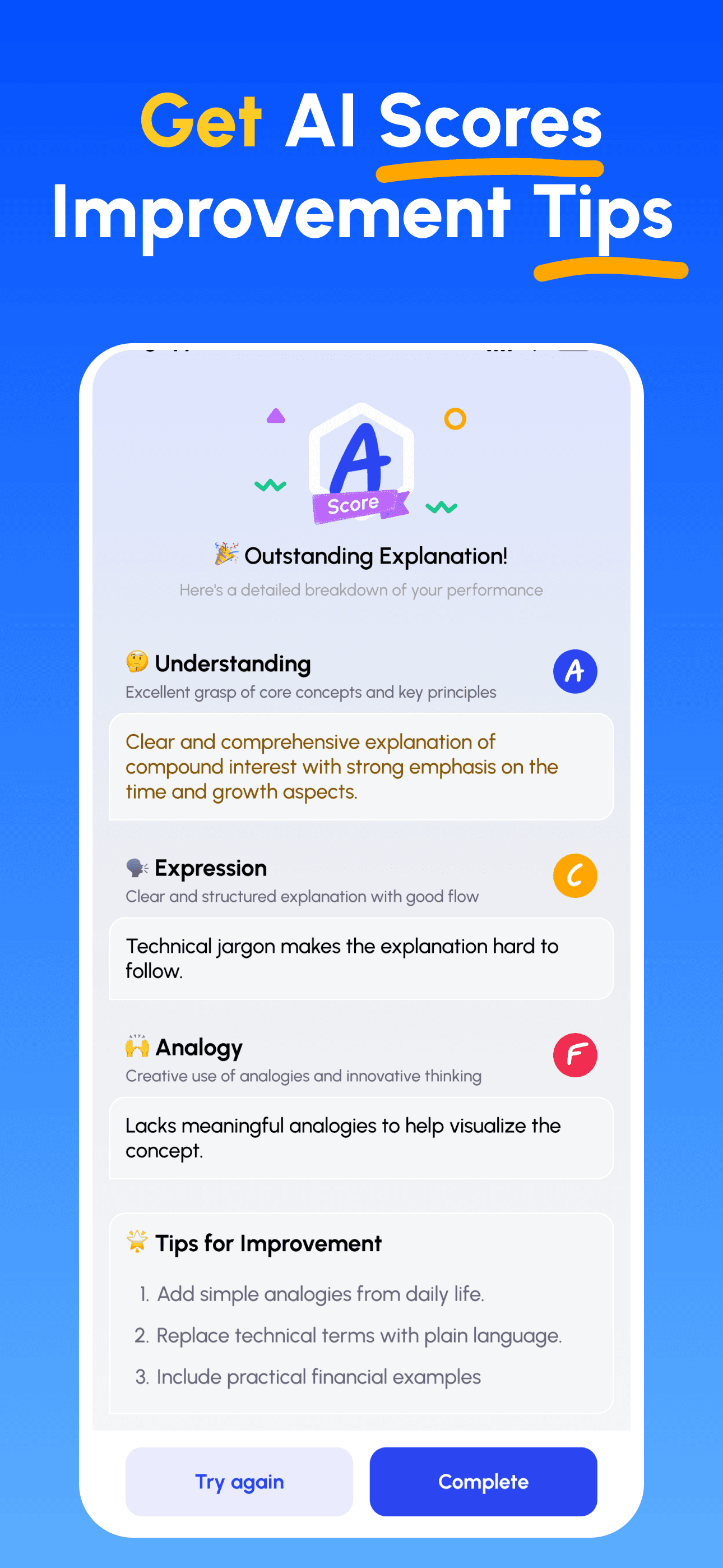
- Professionelle KI-Anleitung erhalten: Erhalten Sie sofortiges, detailliertes Feedback zu Ihrem Verständnis, Ihrer Erklärungsklarheit und Ihren praktischen Anwendungsfähigkeiten.
- Bewertungen prüfen & verbessern: Gezielte Tipps befolgen, Erklärung verfeinern und iterieren, bis Sie es einfach lehren können.
Feynman AI jetzt herunterladen
Starten Sie heute Ihre Reise zu besserer Kommunikation!