Basic Proofs
A proof is like building a path step by step to show why something is true.
簡要介紹
Think of a proof as being a detective who needs to solve a puzzle 🔍. Just like detectives use clues and evidence to reach a conclusion, mathematicians use proofs to show why mathematical statements are true. We start with facts we know are true and use logical steps to reach our final answer.
主要說明
Starting Point 📌
Every proof begins with something we know is true (like given facts or definitions). It's like starting a journey with a map and knowing your starting location.
Logical Steps ➡️
Each step in a proof must follow logically from previous steps. It's like building a bridge - each piece must connect firmly to the previous one.
Clear Reasoning 💭
We must explain why each step is true, just like explaining to a friend why you chose a particular route to get somewhere.
Conclusion 🎯
The proof ends when we reach our target statement. Like completing a puzzle, all pieces must fit together to show the final picture.
範例
- Proving why all squares have four equal sides is like showing someone how to make a perfect sandwich - you start with the definition of a square, then explain step by step why each side must be equal.
- If you want to prove why 2 + 2 = 4, it's like explaining to a child why two pairs of shoes make four shoes - you can physically show them and count.
- Proving that all right angles are 90 degrees is like showing why a door needs to open at exactly that angle to stand straight - you can demonstrate it with real objects and measurements.
費曼AI如何引導你學習
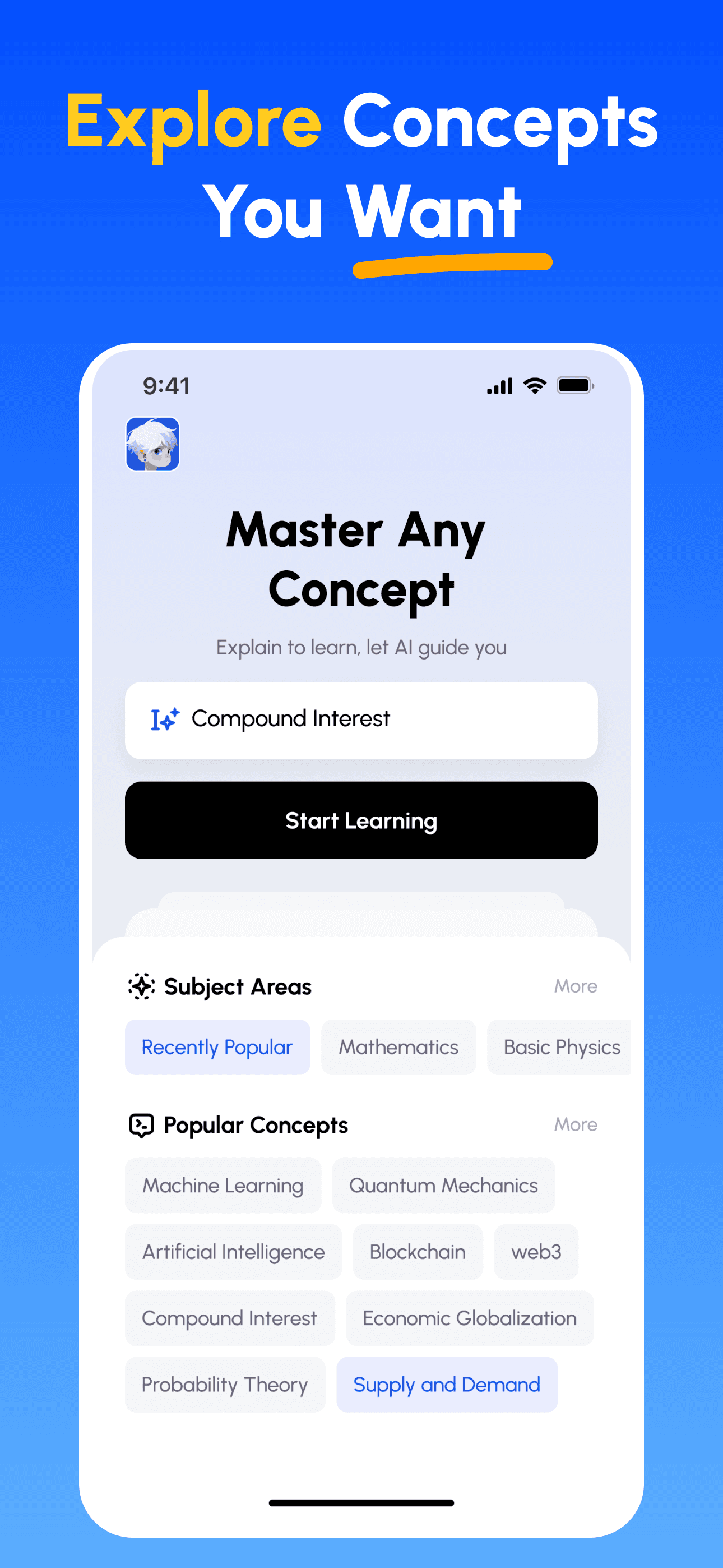
- 選擇任意概念: 從你想掌握的主題開始——瀏覽精選學科或自行輸入。
- 先學核心要點: 用清楚、結構化的解說快速建立知識框架,掌握關鍵與常見誤區。
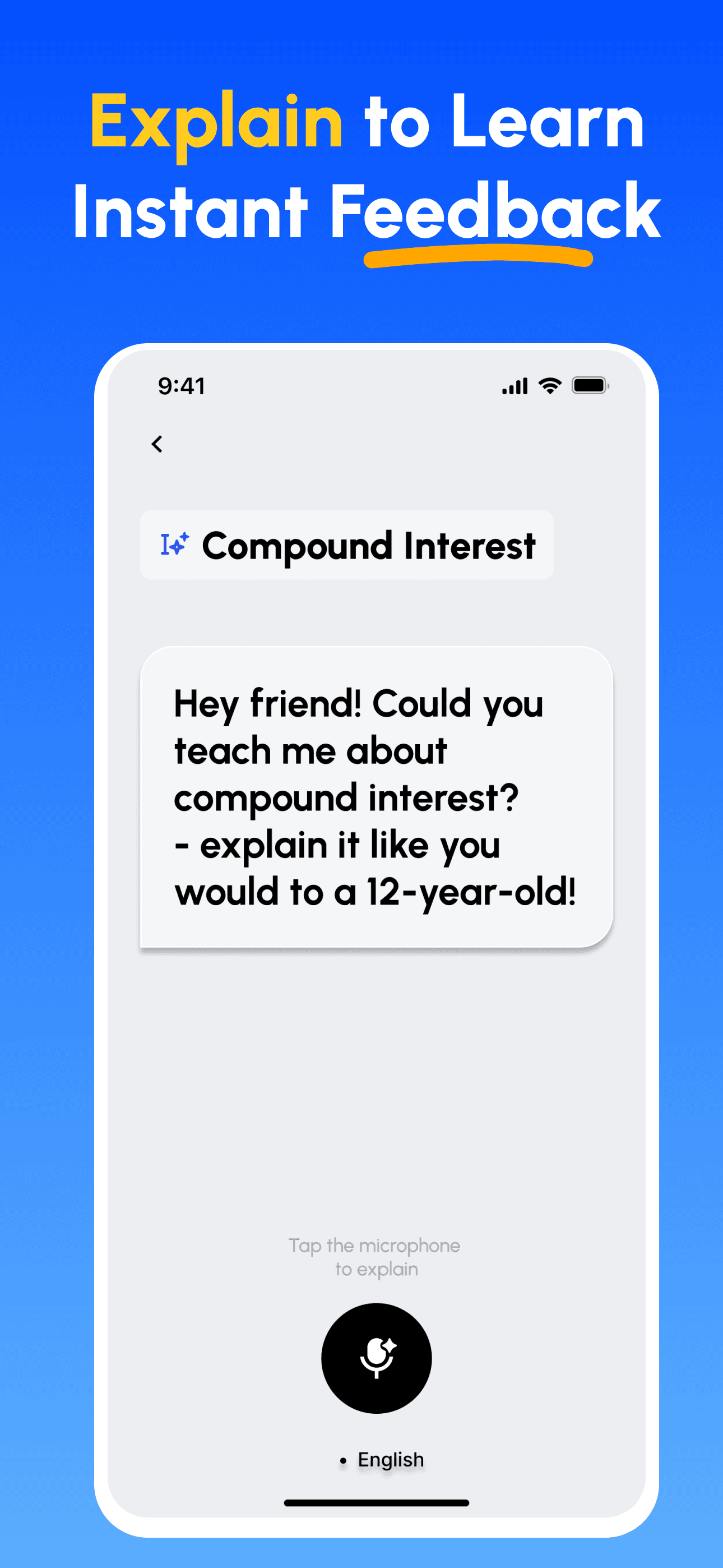
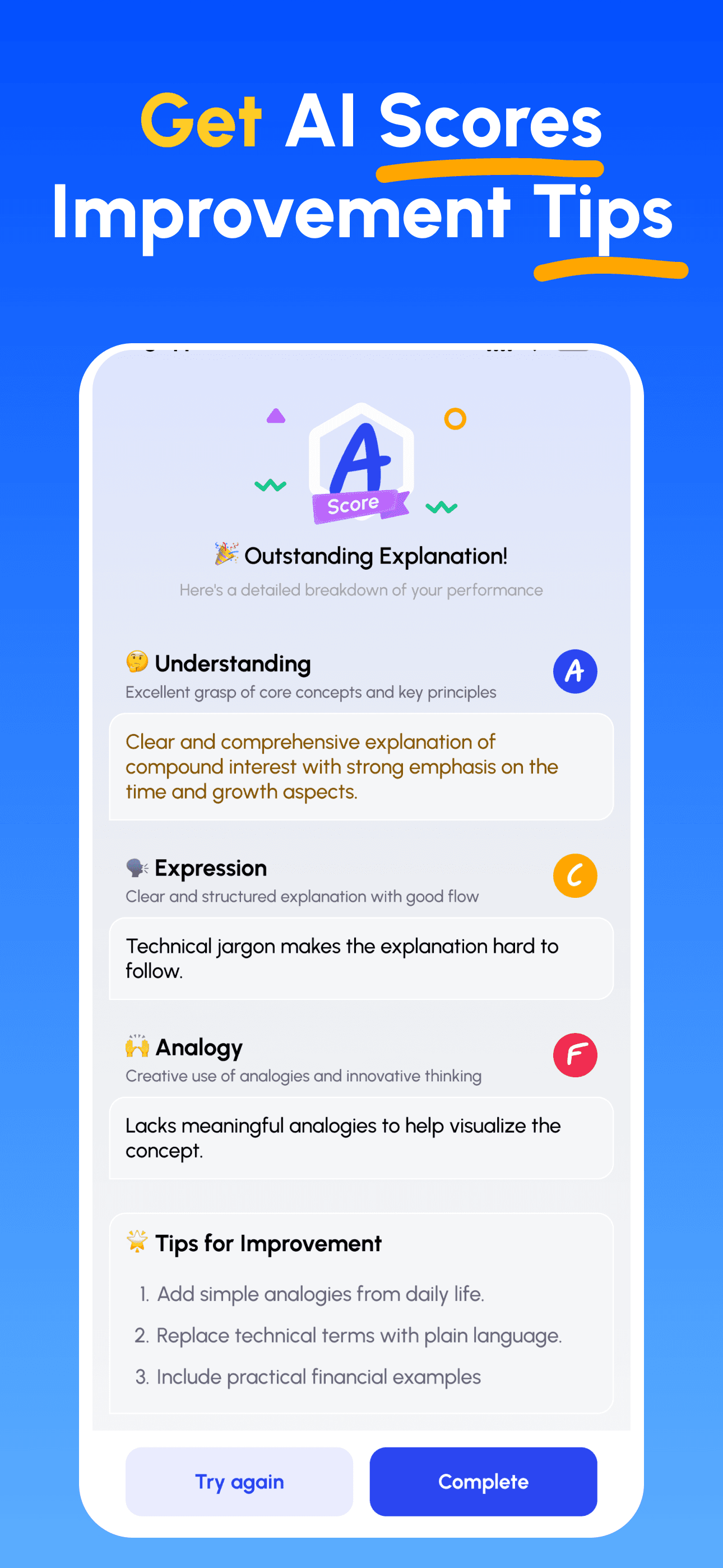
- 講解並獲得回饋: 以語音或文字錄製你的講解;立即取得在深度、清晰度、結構與示例上的分析。
- 檢視評分並精進: 依據針對性建議修正並再講解,直到能簡單講清楚為止。
立即下載費曼AI
今天就開始提升溝通能力的旅程!