Média vs Mediana
Média e mediana são duas formas diferentes de encontrar um valor central em um grupo de números.
Introdução Breve
A média e a mediana são medidas que nos ajudam a entender o comportamento típico de um conjunto de números. 📊 É como se fossem duas formas diferentes de responder à pergunta 'qual é o valor que melhor representa este grupo?'. Enquanto a média considera todos os valores igualmente, a mediana olha para a posição central dos números quando organizados.
Explicação Principal
Média - A soma dividida pelo total 📝
A média é como dividir igualmente algo entre todos. Por exemplo, se 5 amigos juntam R$100 no total, a média seria R$20 para cada um (100 ÷ 5). É como distribuir igualmente todos os valores.
Mediana - O valor do meio 📊
A mediana é o valor que fica exatamente no meio quando organizamos todos os números em ordem. É como fazer uma fila do menor para o maior e escolher quem está no centro.
Quando usar cada uma? 🤔
A média é melhor quando os valores são próximos entre si. A mediana é mais útil quando existem valores muito diferentes (extremos) que poderiam distorcer a média. É como escolher entre dividir um bolo igualmente (média) ou encontrar a pessoa de altura média em uma fila (mediana).
Exemplos
- Imagine as notas de uma turma: 7, 7, 8, 8, 10. A média é 8 (soma tudo e divide por 5) e a mediana também é 8 (o número do meio). Neste caso, ambas representam bem a turma.
- Agora pense nos salários em uma empresa: R$1200, R$1300, R$1500, R$1600, R$15000. A média seria R$4120, mas a mediana é R$1500. Aqui, a mediana representa melhor a realidade da maioria dos funcionários.
- Na idade dos jogadores de um time: 18, 19, 23, 24, 25, 25, 38. A mediana (24) representa melhor a equipe que a média (24,6), pois não é afetada pelo jogador mais velho.
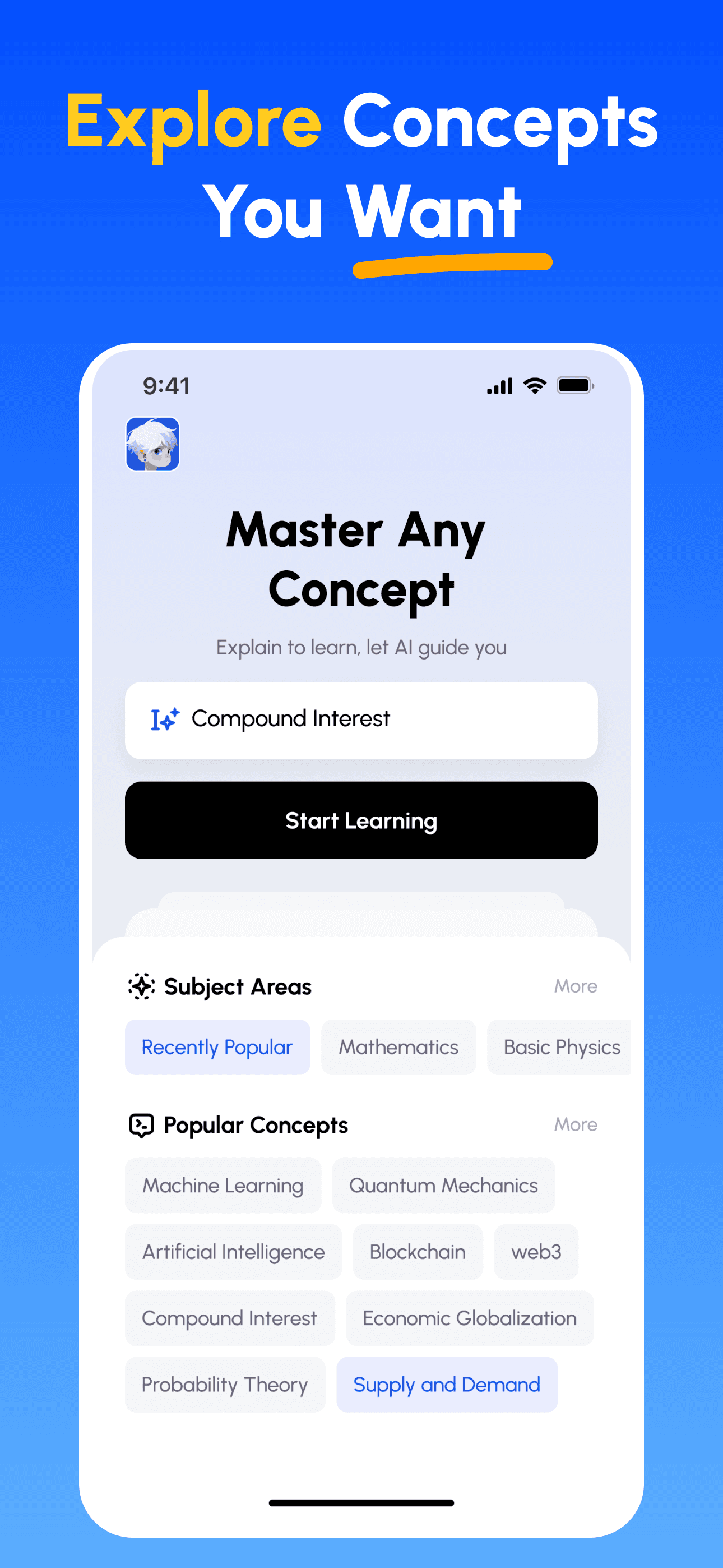
Domine Qualquer Matéria em 3 Passos Simples
- Escolha Seu Objetivo de Aprendizado: Selecione entre centenas de conceitos em ciências, negócios, humanidades e habilidades profissionais. Divida tópicos complexos em partes gerenciáveis.
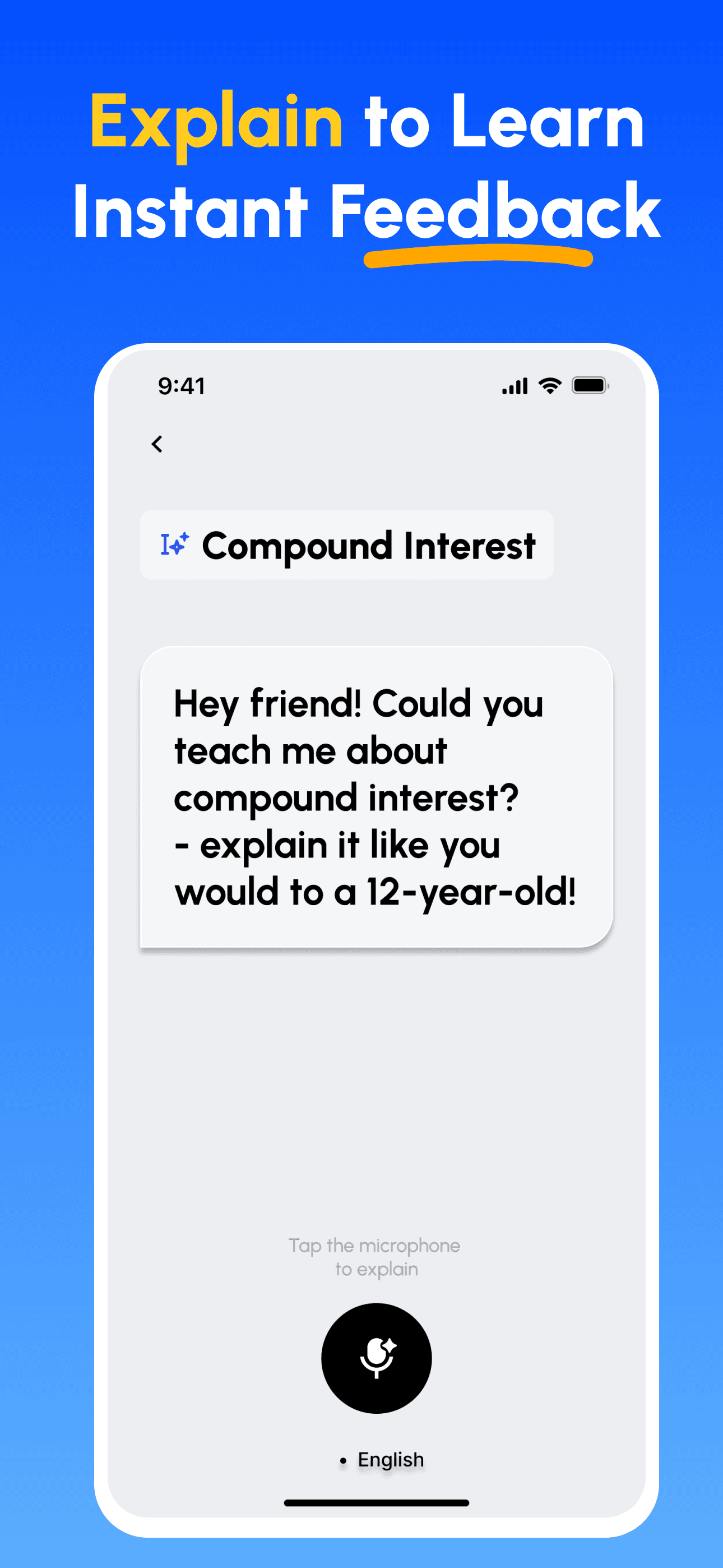
- Aprenda Ensinando: Use nossa plataforma com IA para explicar conceitos como se estivesse ensinando outros. Descubra e preencha lacunas de conhecimento instantaneamente.
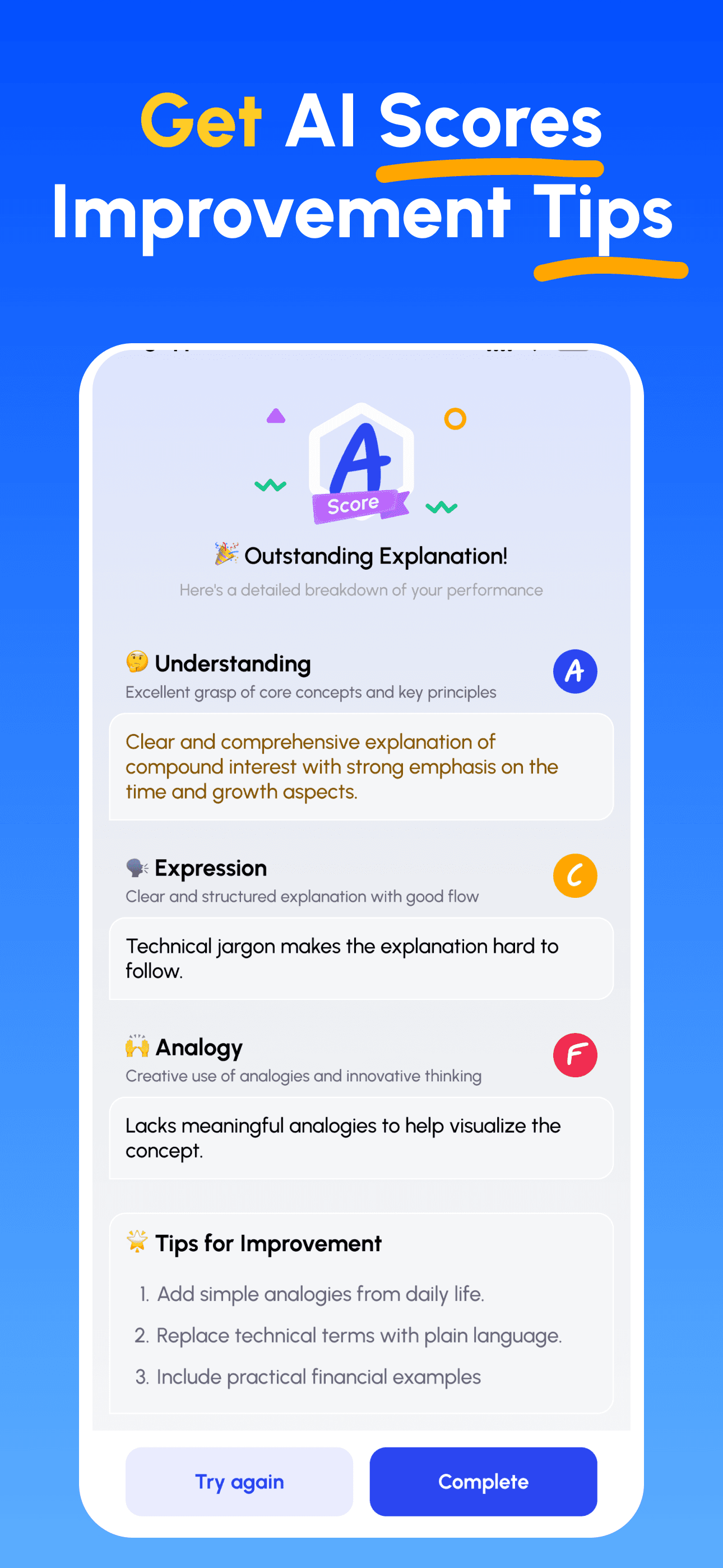
- Receba Orientação Especializada da IA: Obtenha feedback imediato e detalhado sobre sua compreensão, clareza de explicação e habilidades de aplicação prática.
- Revise pontuações e melhore: Siga dicas direcionadas, refine sua explicação e itere até poder ensiná‑la com simplicidade.
Baixe Feynman AI Agora
Comece sua jornada para uma melhor comunicação hoje!