Basic Proofs
A proof is like building a path step by step to show why something is true.
概要
Think of a proof as being a detective who needs to solve a puzzle 🔍. Just like detectives use clues and evidence to reach a conclusion, mathematicians use proofs to show why mathematical statements are true. We start with facts we know are true and use logical steps to reach our final answer.
詳細説明
Starting Point 📌
Every proof begins with something we know is true (like given facts or definitions). It's like starting a journey with a map and knowing your starting location.
Logical Steps ➡️
Each step in a proof must follow logically from previous steps. It's like building a bridge - each piece must connect firmly to the previous one.
Clear Reasoning 💭
We must explain why each step is true, just like explaining to a friend why you chose a particular route to get somewhere.
Conclusion 🎯
The proof ends when we reach our target statement. Like completing a puzzle, all pieces must fit together to show the final picture.
例題
- Proving why all squares have four equal sides is like showing someone how to make a perfect sandwich - you start with the definition of a square, then explain step by step why each side must be equal.
- If you want to prove why 2 + 2 = 4, it's like explaining to a child why two pairs of shoes make four shoes - you can physically show them and count.
- Proving that all right angles are 90 degrees is like showing why a door needs to open at exactly that angle to stand straight - you can demonstrate it with real objects and measurements.
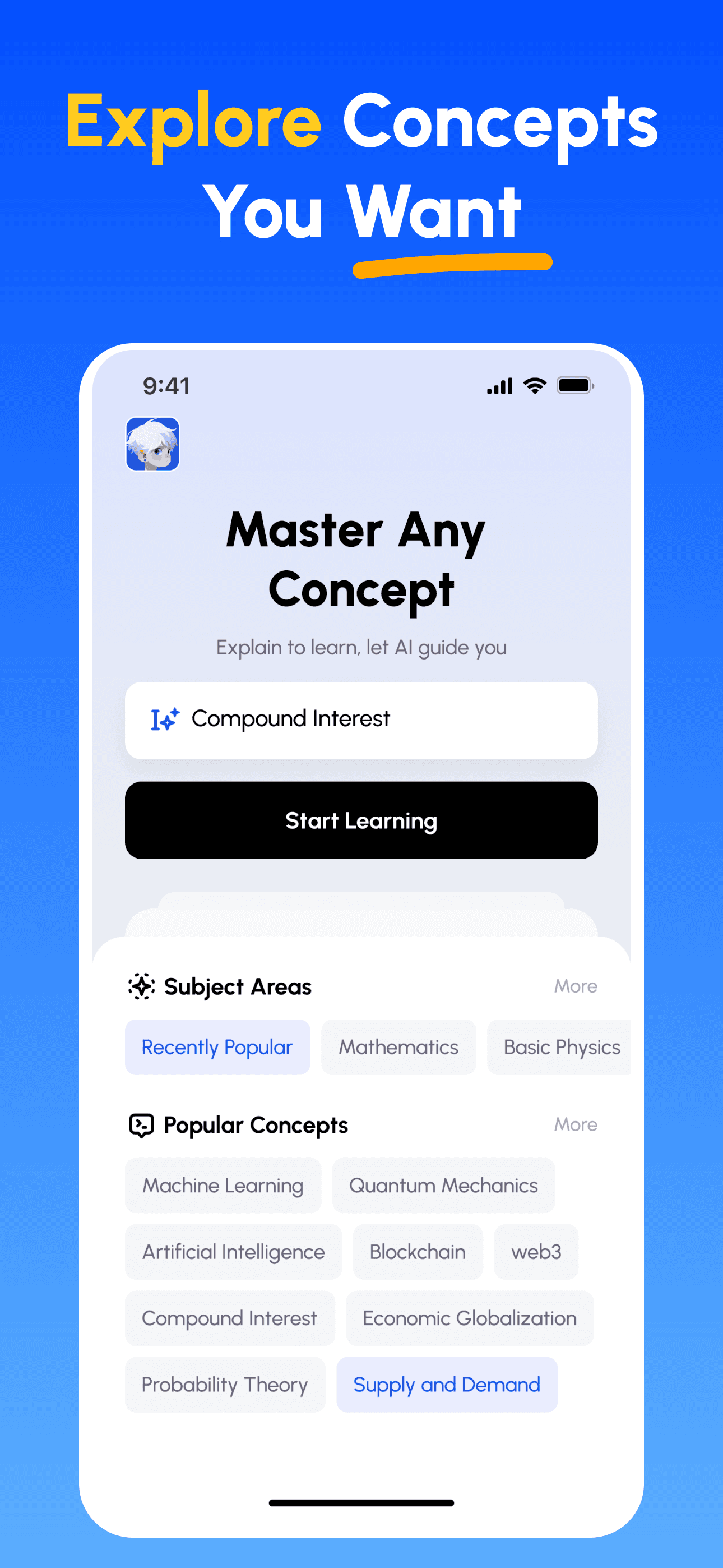
3ステップで確実に習得
- 学習目標を設定: 理系、ビジネス、文系、専門スキルなど、数百の概念から選択。複雑なトピックを理解しやすい単位に分解します。
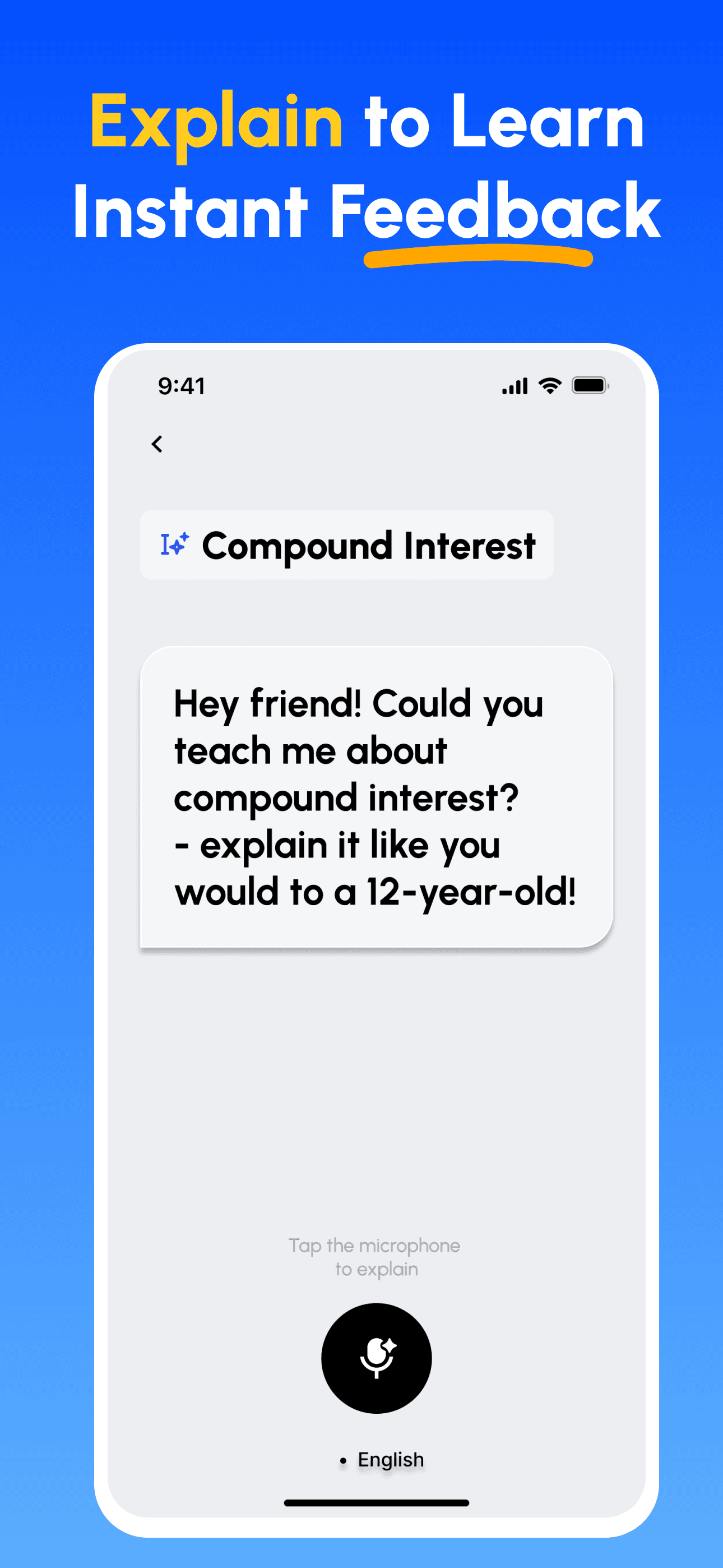
- 教えることで学ぶ: AI搭載プラットフォームを使用して、他者に教えるように概念を説明。知識のギャップを即座に発見し、補完します。
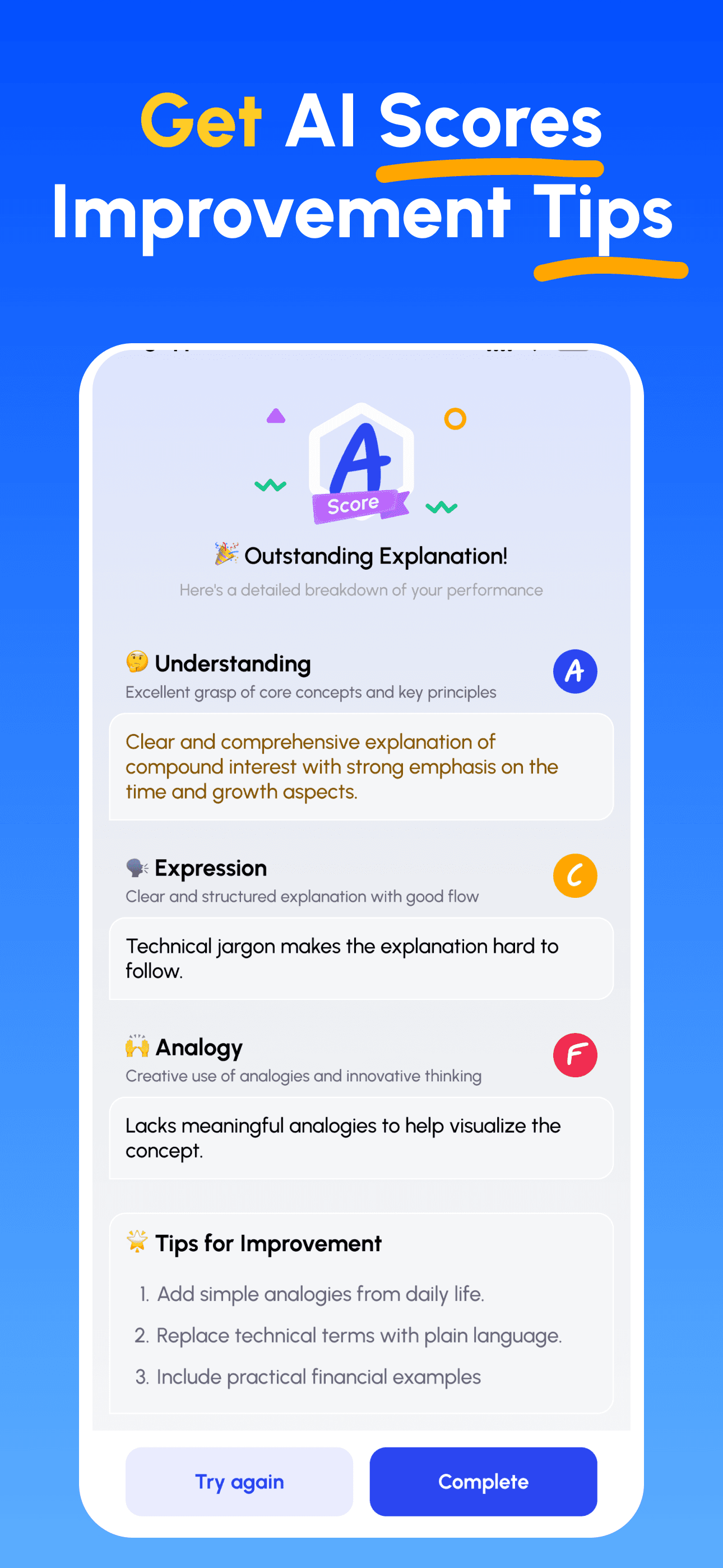
- AIエキスパートガイダンス: 理解度、説明の明確さ、実践的応用力について、即時の詳細なフィードバックを受け取ります。
- スコアを確認して改善: 的確なヒントに従い、説明を磨き、シンプルに教えられるまで反復します。
ファインマンAIを今すぐダウンロード
より良いコミュニケーションへの旅を今日から始めましょう!