Mean vs Median
Mean and median are two different ways to find the middle or typical value in a group of numbers. 📊
簡要介紹
When we have a list of numbers, we often want to find one number that best represents the whole group. The mean (average) and median (middle value) are two common ways to do this. It's like trying to find the typical score in a class or the usual amount of pocket money in a group of friends.
主要說明
Understanding Mean 📈
Mean is like sharing everything equally. If five friends have different amounts of candy (2, 3, 4, 4, 7), adding them all up (20) and dividing by how many friends there are (5) gives you 4 candies each. That's the mean!
Understanding Median 📊
Median is the middle number when values are arranged in order. It's like lining up students by height - the person in the middle is the median height. With numbers 2, 3, 4, 4, 7, the median is 4 (the middle number).
When to Use Each 🤔
Mean is great for balanced data, but can be thrown off by extreme values. If one friend has 100 candies, the mean would jump up dramatically. Median isn't affected by these extreme values, making it better for uneven data like house prices or salaries.
範例
- 🏠 House Prices: In a neighborhood with houses worth $200k, $210k, $220k, $225k, and $1M, the median ($220k) better represents a typical house than the mean ($371k), which is pulled up by the expensive house.
- 📱 Screen Time: If your daily phone usage is 2, 3, 3, 4, and 12 hours, the median (3 hours) better shows your typical usage than the mean (4.8 hours), which is affected by that one long day.
- 💰 Allowance Example: Five kids get weekly allowances of $5, $5, $6, $6, and $20. The mean ($8.40) is misleading, while the median ($6) better shows what most kids receive.
費曼AI如何引導你學習
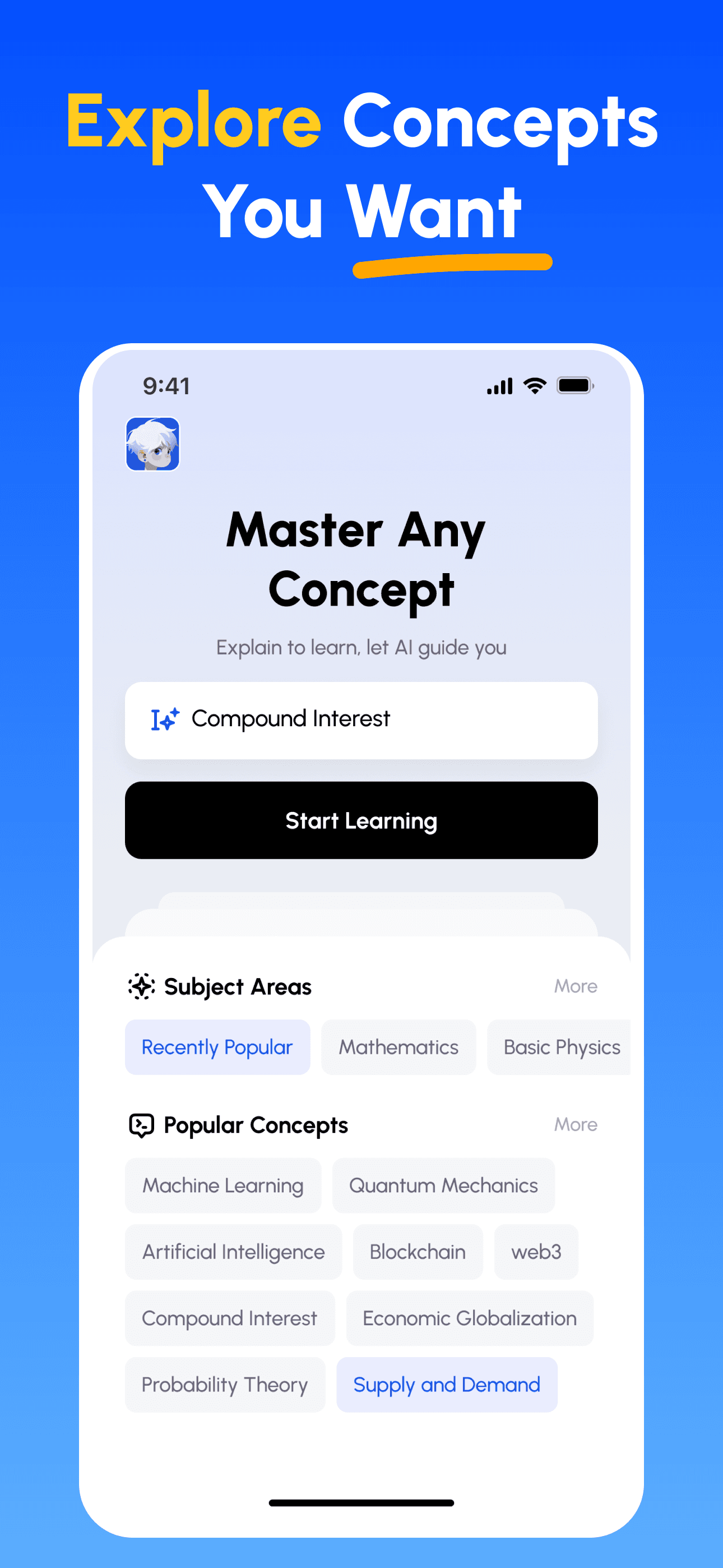
- 選擇任意概念: 從你想掌握的主題開始——瀏覽精選學科或自行輸入。
- 先學核心要點: 用清楚、結構化的解說快速建立知識框架,掌握關鍵與常見誤區。
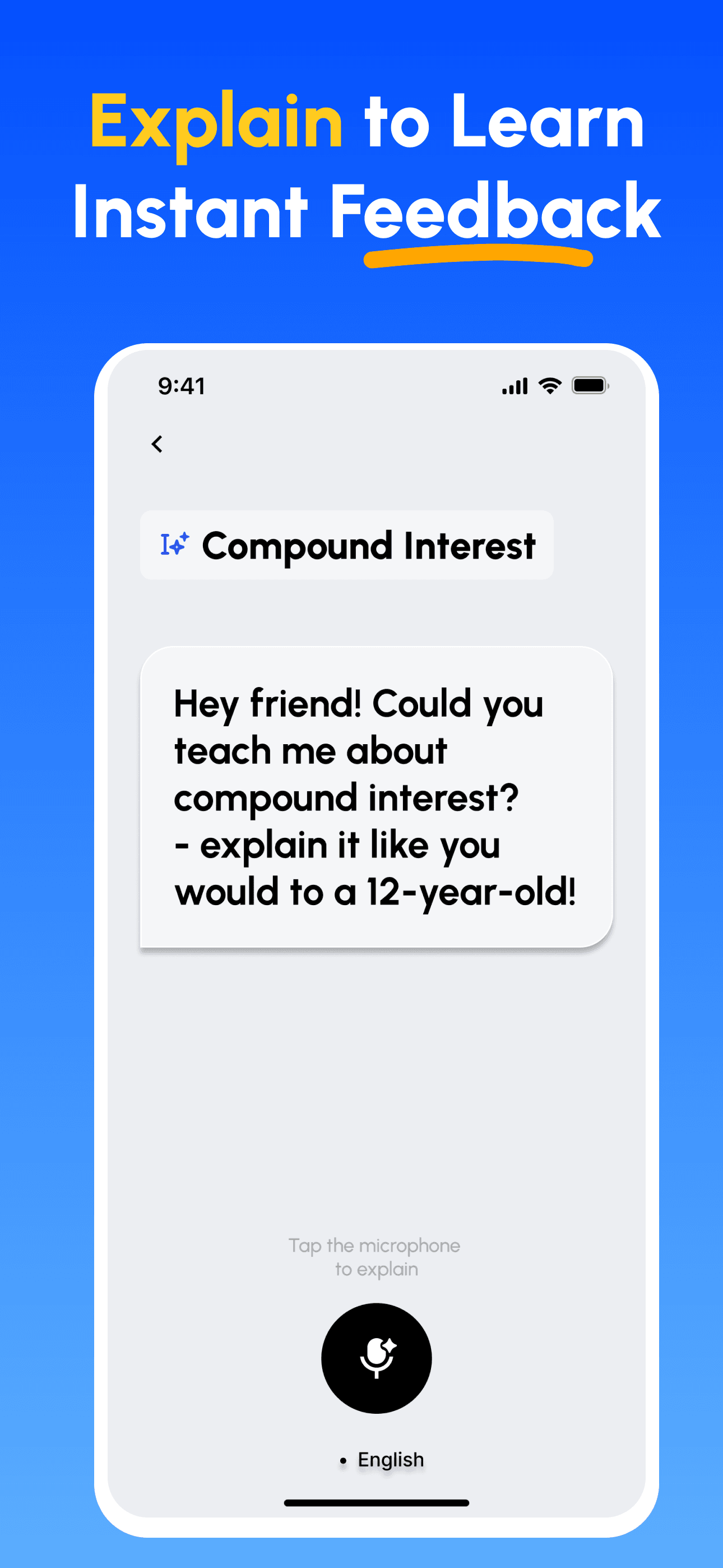
- 講解並獲得回饋: 以語音或文字錄製你的講解;立即取得在深度、清晰度、結構與示例上的分析。
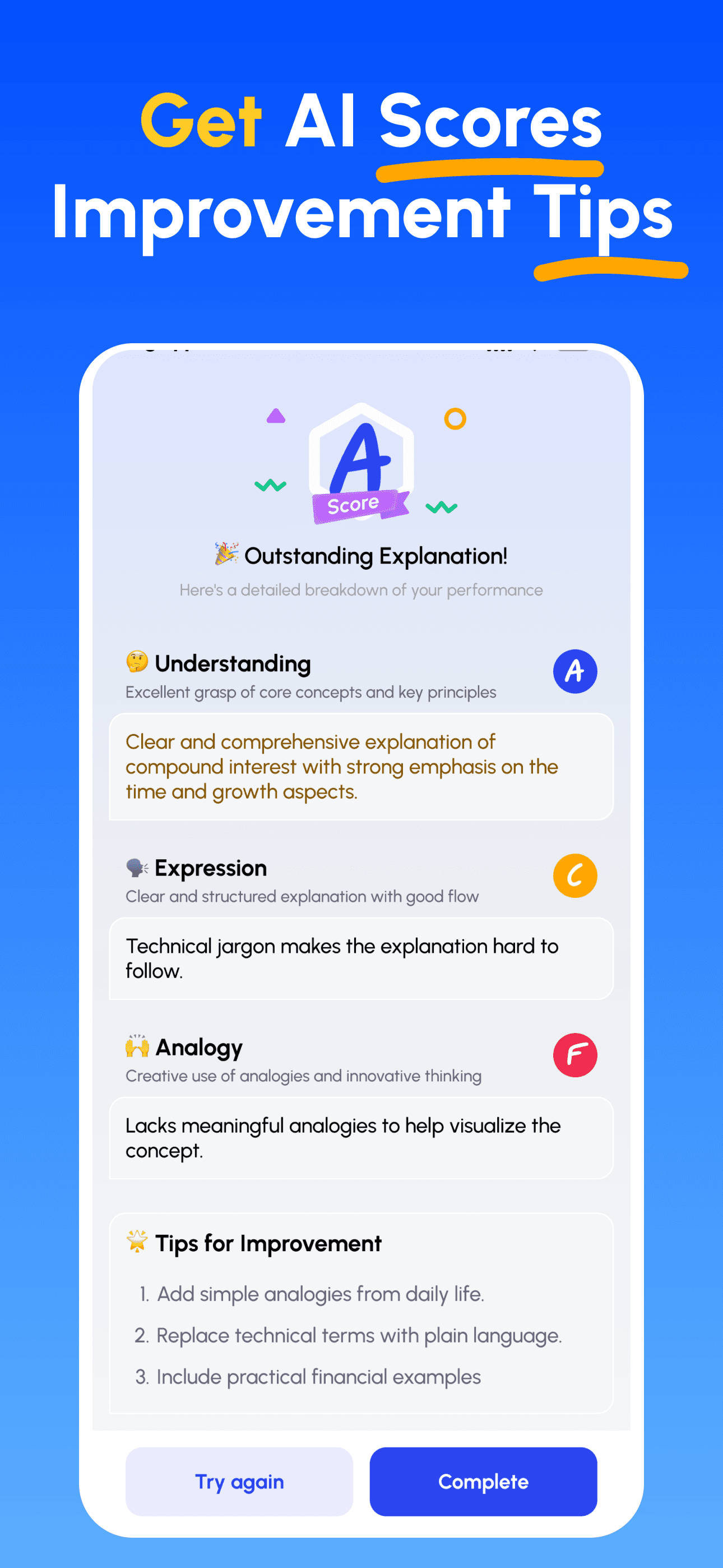
- 檢視評分並精進: 依據針對性建議修正並再講解,直到能簡單講清楚為止。
立即下載費曼AI
今天就開始提升溝通能力的旅程!